电机概念及分类介绍

一、电机概念介绍

从广义上讲，电机是电能的变换装置，包括旋转电机和静止电机。旋转电机是根据电磁感应原理实现电能与机械能之间相互转换的一种能量转换装置；静止电机是根据电磁感应定律和磁势平衡原理实现电压变化的一种电磁装置，也称其为变压器。

这里主要介绍旋转电机，旋转电机的种类很多，在现代工业领域中应用及其广泛，可以说，有电能应用的场合都会有旋转电机的身影。

图一：伺服电机

二、电机分类及应用概述

众所周知，电机是传动及控制系统中的重要组成部分，随着现代科学技术的发展，电机在实际应用中的重点已经从过去简单的传动向复杂的控制转移；尤其是对电机的速度、位置、转矩的精确控制。但电机根据不同的应用会有不同的设计和驱动方式。因此人们根据旋转电机的用途，进行了基本的分类。

图二：旋转电机的分类

三、伺服电机

伺服电机广泛应用于各种控制系统中，能够将输入的电压信号转换为电机轴上的机械输出量，拖动被控元件，从而达到控制目的。

伺服电机的应用现状：

    橡胶轮胎行业：轮弹簧钢丝机、线切割机、铝包钢丝机等。

    食品行业：糖度显示仪、大型烤箱、咖啡机等。

    服装行业：三菱高头机、纺纱机、电脑绣花机、印花机。

图三：绣花机电机

四、步进电机

步进电机是一种将电脉冲转化为角位移的执行机构；通俗来说就是当步进电机驱动器接收到一个脉冲信号时，它就会驱动步进电机按设定的方向转动一个固定的角度。

步进电机的应用现状：

    数控机床制造领域、自动送料机、软盘驱动器、打印机、绘图仪、工业机器手、包装机械、汽车测试等。

图四：软盘驱动器

五、力矩电机

力矩电机是一种扁平形多极永磁直流电机。其电枢有较多的槽数、换向片数和串联导体数，以降低转矩脉动和转速脉动。力矩电机有直流力矩电机和交流力矩电机两种。

力矩电机的应用现状：

交流力矩电机又可以分为同步和异步两种，目前常用的是鼠笼型异步力矩电动机，它具有低转速和大力矩的特点。一般在纺织工业中经常使用交流力矩电机。

图五：力矩电机

六、开关磁阻电机

开关磁阻电机是一种新型调速电机，结构及其简单且坚固，成本低，调速性能优异，是传统控制电动机强有力竞争者，具有强大的市场潜力。    

开关磁阻电机的应用现状：

    开关磁阻电机被应用于龙门刨床、锻压机床、纺织机械、造纸机、球磨机、风机

压缩机、抽烟机等。

     图六：车用开关磁阻电机

七、无刷直流电机

无刷直流电机是在有刷直流电机的基础上发展起来的，但它的驱动电流是不折不扣的交流。无刷直流电机为了减少转动惯量，通常采用细长的结构。无刷直流电机在重量和体积上要比有刷直流电机小的多。

无刷直流电机的应用现状：

无刷直流电机的应用十分广泛，如汽车、工具、工业工控、自动化以及航空航天等等。具体可分为以下三种主要用途，第一：持续负载应用，如风扇、抽水机、吹风机。第二：可变负载应用，如油泵控制、发动机控制等。第三：定位应用，应用在大多数工业控制。

图七：无刷直流电机

八、直流电机

直流电机是出现最早的电机，大约在19世纪末，其大致可分为有换向器和无换向器两大类。直流电机有较好的控制特性。直流电机在结构、价格、维护方面都不如交流电机，但直流电机具有调速性能好、启动容易、可载重启动等优点而被广泛应用。

直流电机的应用现状：

    生活方面，被用于很多电动产品，如风扇、刮胡刀等。在宾馆中，自动门、自动门锁、自动窗帘都用到直流电机。直流电机还广泛应用于飞机、坦克、雷达等武器装备中。直流电机还可应用于机车牵引、如铁路机车直流牵引电机、地铁机车直流牵引电机等。

图八：Z4直流电机

九、交流电机

异步电机是基于气隙旋转磁场与转子绕组感应电流相互作用产生电磁转矩而实现能量转换的一种交流电机。异步电机具有结构简单，制造、使用和维护方便，运行可靠及质量较小，成本较低等优点。     

异步电机的应用现状：

    在异步电机中较为常见的是单相异步电机和三相异步电机，其中三相异步电机是异步电机的主体。三相异步电机可用于驱动压缩机、水泵、破碎机等，还可用于传动鼓风机、磨煤机、轧钢机、卷扬机等。单相异步电机在家用电气中使用较多，如电扇、冰箱、空调等。

图九：风机、冰柜电机

十、同步电机

同步电机就是在交流电的驱动下，转子和定子的旋转磁场同步运行的电机。同步电机的定子和异步电机的完全一样，但同步电机的转子有“凸极式”和“隐极式”两种。     

同步电机的应用现状：

    同步电机主要用于大型机械，如鼓风机、水泵、球磨机、压缩机、轧钢机以及小型、微型仪器设备或者充当控制元件，三相同步电机是主体。同步电机还可以当调相机使用，用于向电网输送感性或者电容性无功功率。

图十：同步电机组成

十一、旋转变压器

旋转变压器是一种电磁式传感器，也称同步分解器，它是一种测量角度用的小型交流电动机，用来测量旋转物体的转轴角位移和角速度，由定子和转子组成。    

旋转变压器的应用现状：

旋转变压器是一种精密角度、位置、速度检测装置，适用于所有使用旋转编码器的场合，特别是高温、严寒、潮湿、高速、高震动等旋转编码器无法正常工作的场合。它可完全替代光电编码器、在机器人系统、机械工具、汽车、电力、航空航天等位置检测系统中。也可用于坐标变化、三角运算和角度数据传输、作为两相移相器用在角度--数字转换装置中。

图十一：旋转变压器

十二、感应同步器

感应同步器将角度或直线位移信号变换为交流电压的位移传感器又被称为平面式旋转变压器。它有圆盘式和直线式两种。在高精度数字显示系统或数控闭环系统中圆盘式用于检测角位移信号，直线式用

于检测线位移。

感应同步器的应用现状：

    被广泛用于大位移静态与动态测量中，如三坐标测量机、程控数控机床及高精

度重型机床及加工中心测量装置。

图十二：感应同步器

十三、自整角机

自整角机是利用自整步特性将转角变为交流电压或交流电压变为转角的感应式微型电机，在伺服系统中被用作测量角度的位移传感器。自整角机还可用于实现角度信号的远距离传输、变换、接收和指示。

自整角机的应用现状：

被自整角机还可用于实现角度信号的远距离传输、变换、接收和指示。它被广泛用于冶金、航海等位置和方位同步指示系统和火炮、雷达等伺服系统中。

图十三：自整角机

十四、速度信号电机

最具代表性的速度信号电机是测速发电机，实质上是一种将转速变换为电信号的机电磁元件，其输出电压与转速成正比。

速度信号电机的应用现状：

测速发电机在控制系统中主要作为阻尼元件、微分元件、积分元件和测速元件来使用。

图十四：测速发电机

图十五：电机分类图

电机控制中矢量图的作用

一、前言

在电机驱动开发过程中，我们有的时候需要知道相电压与线电压之间的关系，也可能会需要知道相反电动势与线反电动势之间的关系等，那么为了能够直观的分析出这些矢量的关系（包括幅值关系、相位关系），我们就可以借助矢量图这个工具了。

利用矢量图，我们可以很容易根据矢量合成及矢量分解的法则来得出要分析的矢量之间的关系，就可以用几何加数学的方式找出合成矢量所处的位置或者合成矢量被分解之后的位置。我们甚至通过矢量图的关系分析之后，再根据反电动势跟转子位置的关系可以得出转子的位置。因此我们了解矢量图及其相关的法则就很有必要了。如下图一所示为三相坐标系的坐标图示意图：

图一：三相坐标系坐标示意图

二、矢量概念介绍

想要学会分析矢量图，我们需要有一些基础知识的铺垫，这里我们有必要简单介绍一下矢量的概念。矢量这个概念其实最早可以追溯到我们中学课堂里学过的向量，我们都知道，向量是一个既有大小又有方向的量，向量的运算不在遵循一般的四则运算法则，而是有专门的运算方式，下图二所示为我们中学向量的表示方式：

图二：向量的表示示意图

而矢量这个概念其实到大学课本才接触到，它的定义是，有的物理量，既要有数值大小，又要有方向才能确定完全确定。这些量不遵循一般的代数法则，而遵循特殊的运算法则。这样的量被称为物理矢量。其实向量这个概念在数学课本用得比较多，在物理课程中就有了另一个名字“矢量”。只不过在物理学中，会有很多物理量如力，它有大小和方向，电压，也有大小和方向，用来表示物理量的大小和方向就被称为了矢量，而数学只是研究某个有方向和大小的量的运算及表示形式，因此就把它称为了向量。所以，对于我们工程师来说，可以理解它们就是一个东西。

三、矢量的运算法则

矢量之间的运算要遵循特殊的法则。矢量的加法可以一般可以使用平行四边形法则，当然也可以推广到三角形法则或者正交分解法。矢量减法是矢量加法的逆运算，一个矢量减去另一个矢量，等于加上那个矢量的负矢量。

矢量也可以进行乘法运算，矢量和标量的乘积仍为矢量，矢量和矢量相乘，可以得到一个新的标量（只有大小，没有方向的量），这样得到的结果是标积；两个矢量相乘也可以得到一个新的矢量，把这样的乘法称为矢积。其实就对应着中学课本中学习的向量的内积和外积。

图三：矢量加法的平行四边形法则示意图

图四：矢量减法法则示意图

图五：矢量的正交分解法示意图

在电机控制中，基本上以上三种方式使用得比较多，其实在遇到减法得场合，都是转换为加法进行合成。

四、反电动势矢量合成

在电机控制系统中，我们可以基于定子三相绕组建立三相基本坐标系，在这个坐标系中可以进行矢量合成与分解的分析，从而可以知道反电动势之间的关系。

图六：反电动势矢量合成示意图

如上图六所示，我们知道了Ea及-Eb相反电动势的大小及方向，利用平行四边形的法则可以得出线反电动势的的大小及方向。在上图坐标系中，我们假设顺时针旋转为角度超前，从上图中可以得出先线电动势Eab超前相反电动势-Eb 30度，相反电动势Ea超前线反电动势Eab 30度。还可以根据三角形的关系将合成得到的线反电动势跟相反电动势的幅值关系求出来。

在SPWM及SVPWM算法中，我们就需要知道相电压跟线电压的关系，从而推导出两种算法的电压利用率问题，所以我们了解矢量图的合成与分解原理，就可以很方便的知道矢量的关系，也可以很好的分析出电压利用率的问题。下图七给大家展示了一幅完整的全坐标系内的反电动势合成矢量图：

图七：全坐标系内反电动势合成示意图

有了这幅图，大家可以很好的分析出各种情况下的相反电动势和线反电动势之间的关系。当我们需要推导三相电机六步换相的绕组通电顺序的时候，就可以根据霍尔信号与线反电动势之间的关系，推导出霍尔信号跟相反电动势的关系，从而确定出正确的通电顺序。

五、总结

通过这篇文章，只想跟大家分享矢量图在我们电机控制中的作用，文章中简单的列举了个别合成示意图，只是希望大家能够掌握这种方法，后期自己在电机控制开发过程中能够举一反三，利用好矢量图这个工具去分析自己遇到的情况，能够快速的得出矢量之间的关系，有助与项目开发的进度。

反电动势到底该如何来理解？

电机中的反电动势是如何产生的呢？要了解这个问题，我们需要回顾一下高中时学过的电磁学知识，在电磁学中我们学到过感应电动势，感应电动势又分为动生电动势和感生电动势两类。

动生电动势是一种由于导体在磁场中运动而在导体内部产生的电动势。感生电动势是一种由于磁场变化而静止导体中产生的一种电动势。

那么我们直流无刷电机中产生的反电动势属于感应电动势中的哪一类呢？因此我们就需要了解一下直流无刷电机的构造了。下图一是一个外转子直流无刷电机：

图一：外转子直流无刷电机示意图

那么从上图一中的电机组成来看，我们知道定子是线圈组成，也就是说导体是静止的，而转子由永磁体组成，永磁体是转动的，那么当永磁体转动时，对于线圈来说就是线圈的磁场发生了变化，因此对于这样构造的直流无刷电机来说，产生的感应电动势就是感生电动势。我们也可以知道，感生电动势的产生是转子永磁体对定子线圈的一个作用。

从上面我们知道，随着电机转子（永磁体）的转动，会感生出一个感生电动势，这个感生电动势的方向可以根据楞次定律（感应电流的磁场总要阻碍引起感应电流的磁通量的变化）来进行判断。

图二：外加磁场靠近线圈，磁通量增加时感应电动势方向示意图

图三：外加磁场远离线圈，磁通量减小时感应电动势方向示意图

从上图二图三我们可以知道，当线圈磁通量增加，感应电流产生的磁场方向要阻碍磁通量的增加，当线圈磁通量减小时，感应电流产生的磁场方向要阻碍磁通量的减小。

那么这个感应电动势的方向跟线圈外加电压的方向是相反的，所以通常在电机中把这个感应电动势称为反电动势。这就是反电动势的来源。

通过以上分析，我们知道了转子是永磁体，定子是绕组线圈的直流无刷电机产生的感生电动势就是电机的反电动势，那么根据感生电动势E的公式：

由以上公式可以知道电机绕组中的反电动势的大小跟它的单位时间内的磁通量的变化量成正比。也就是说，在Δt固定的情况下，磁通量变化越大，那么反电动势就越大，反之磁通量变化越小，那么反电动势就越小。

我们知道磁通量的公式如下：

其中，B是磁感应强度，S是线圈平面面积，θ是线圈平面法线与磁感应强度B的夹角。

图四：坐标系及角度定义示意图

为了方便分析，我们假设坐标系及角度定义如上图四所示，从磁通量公式我们可以知道，定子绕组中的磁通量是按正弦规律变化的。

图五：转子与定子线圈通电示意图

在上图五中，转子永磁体磁力线方向与N方向一致，而线圈平面法线方向水平向右，如下图六所示：

图六：磁感应强度方向与线圈平面法线方向示意图

我们可以根据磁通量的公式知道，此时线圈磁通量为0。

图七：转子与定子线圈通电示意图

当转子转动到上图七所示的位置时，此时夹角θ为0，根据磁通量的公式可知，此时磁通量是最大的，因此对于一个固定的定子绕组来说，当转子转动一周，随着磁感应强度与线圈平面的夹角不同（也就是转子的位置角不同）那么磁通量的变化是按照正弦规律变化的。

图八：磁通量曲线示意图

从图八我们可以知道，在0度位置时，磁通量最大，但是磁通量的变化率最小为0（斜率为0），感应电动势为0，在90度时，磁通量为0，但是磁通量的变化率最大（斜率最大），感应电动势最大，在180度时，磁通量最大，磁通量的变化率又为0（斜率为0），感应电动势为0，在270度时，磁通量为0，但是磁通量的变化率最大（斜率反向最大），感应电动势最大。

也就是上式中为单位时间内的磁通量变化，这个变化在数学中可以用求导来表示，也即是上式我们可以写成为：

因此我们可以根据上式画出感应电动势（反电动势）的波形，如下图九所示：

图九：感应电动势波形示意图

那么以上就是对电机中的反电动势的一些理解，仅供大家参考，起个抛砖引玉的作用，希望大家可以利用以上分析，对反电动势的理解更加深入、更加透彻、更加清晰。本篇文章就给大家分享到这里，谢谢大家！

直流电机驱动PCB设计注意事项讲解

一、 项目名称：《直流电机驱动器设计》

二、 直流有刷电机驱动PCB设计注意事项讲解

大家好，经过前面文章的分享，原理图我们已经全部设计完毕了，接下来需要绘制PCB了，那么在绘制PCB之前，我们需要给原理图中各个元器件都添加上对应的封装，这样就可以将带有电气属性的各个元器件导入到绘制PCB的界面中了。

图1：项目原理图

我们将上图中的所有元器件都导入到PCB绘制文件中，可以看到下图所示的样子：

图2：网表导入

导入之后，就需要对元器件布局，再按照设置的规则进行布线，当布线全部完成之后，可以进行PCB的覆铜，覆铜结束之后可以添加泪滴，最后DRC检查下是否有违背电气规则的地方，整个PCB就绘制完毕了。

PCB绘制完毕之后，需要发给PCB加工厂家进行PCB板的制作，接下来是焊接、调试、测试等流程，直到整个项目功能完成。

那么，关于PCB绘制部分，就有如下流程可供大家参考：

① 网表导入

② 板框设置

③ 电气规则设置

④ 元器件布局

⑤ 布线

⑥ 覆铜

⑦ DRC规则检查

⑧ Gerber文件生成

⑨ 发板

那么，在以上9个部分的内容中，其实④⑤⑥这三部分是比较重要的，尤其是第④部分元器件布局，我们说好的布局能让后面的走线变得比较顺畅，能让整个PCB绘制变得事半功倍，所以布局在整个PCB绘制中是占了很高的比重的。

接下来我们就来谈谈布局的注意事项：

第一：输入和输出要分开。也就是说我们在布局的时候，要划分好输入和输出，在元器件摆放的时候，输入部分和输出部分的器件应该分开摆放，不要放在一个方向。比如说输入放在左边，那么输出可以放在右边，输入放在上边，输出可以放在下边，遵循这样的原则来进行布局。

图3：输入输出布局方向示意图

第二：高压和低压要分开。板子上的高压和低压需要进行分隔，不能混在一起，比如说当项目中的母线电压是310V的时候，然后单片机部分是3.3V，如果这两个电源不分开的话，那么就很容易出问题，导致单片机损坏。

图4：高压和低压划分示意图

第三：功率和信号要分开。就是功率部分和信号部分要分开，不要混在一起，如果混在一起的话，就会导致功率部分可能会将信号部分干扰，这样会导致控制逻辑出现混乱。

第四：需要考虑回路，回路尽量越短越好。这个布局原则需要结合原理图考虑，在摆放元器件的时候就要反复斟酌，回路是怎么走的？怎么摆放才能使回路路径是最短的？但是这个原则有时候往往又是比较难做到的，因为有时候回路虽然是最短的，但是走线又不好走了，所以只能是确保回路尽量最短。就好比我们电机驱动的功率部分，因为有功率管的开关，而开关的频率一般在几十KHz，如果回路的面积大的话，回路上可能会产生很多寄生参数，导致振荡的发生，也可一定程度上抑制EMI的产生。

以上就是布局的注意事项，大家在布局的时候需要遵循这几点来考虑。

接下来我们来看下走线的注意事项。

第一：走线尽量走钝角。大家要知道走线是流过电流的，那么电流大家可以跟河流的水流联系起来，如果水流正常情况下流动很顺畅，这时候突然来了一个大拐角，此时水流会在急弯处发生方向突变，这样的话就会引起振荡了，在拐角处就很容易溅起水花。同样的电流也一样，如果出现了锐角走线，那么也会有类似的效果。

图5：锐角走线示意图

第二：尽量少用过孔。其实我们在走线的时候，要尽量追求顺畅的，毕竟过孔他就是一个结点，一个结点的阻抗与走线的阻抗是不一样的，可能还存在更大的寄生参数，如果可以不用过孔，就不用了。

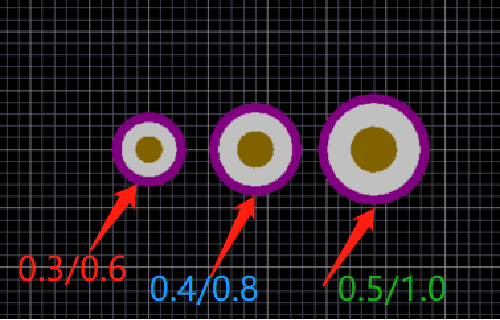
第三：过孔大小要统一。0.3/0.6 0.4/0.8 0.5/1.0 这种过孔比较常见，厂家在生产 PCB 的时候，如果你的过孔的型号越多啊，那么制作的时间肯定是越长的，我们尽量做到统一，如果过孔一个钻头钻到底，那么时间也节约了，板子也好看了，另外，过孔的大小啊，尽量是 0.3，0.4 类似于这样的大小。不要什么 0.31 0.32 这样的，板厂都没有这样的钻头，引来不必要的麻烦。

图6：过孔型号示意图

第四：走线尽量要顺畅美观。越顺越好，比如我们画一天时间也可以画，画一星期也是画，但是顺畅度和美观度肯定是不一样的，首先顺畅度是排首要，然后就是美观度，电流其实真的类比于水流，越顺越好，至于美观的画不用我说，都知道，在一家公司工作我们必须注意自己的个人品牌，不要被人说，谁谁画的板子，就是丑死了。

第五：尽量使用贴片封装。这个的话就是板子美观，然后板子加工成本更低，省钱。在 N 年前，大家都尽量用插件的，后来随着贴片机的普及，贴片价格的便宜，人工成本的上涨，都从插件往贴片过渡了，现在的人工成本很高的。

第六：线径大小要统一。比如说信号线，我们尽量都设置为一个规格，例如都设置为0.3mm。另外走大电流的线，不要突然变大或者突然变小。这样突变的话，就好比流水的渠道忽大忽小，就很容易水流的涟漪，对电流的话就是振荡，这样对EMI是很不好的。

图7：线径突变

第七：元器件的方向尽量要一致。打个比方啊，电解电容不是分正负极吗？如果朝向乱七八糟，各个方向都有，对于工人来说，当然是尽量插对啊，但是方向很乱各个方向都有的话，是不是有时候一不小心插错方向的可能性更大呢？另外一个方面就是，生产的时候，波峰焊的问题。

图8：元件朝向示意图

例如上图，我们推荐使用上图中的上面的摆放方式，这样生产出来的产品会更好。

最后，我们再说下地线，我们说地线其实是有分类的，并不能所有的地都铺成一个整体的平面，而是需要根据功率的不同进行划分。例如我们可以划分为总地和分地。总地的话，就是输入大电解电容的地，而其它芯片的地就是分地。其它分地之间的连接需要做好划分，最后再跟总地进行连接。

图9：地的连接示意图

大家看上图，H桥功率部分的地和下面单片机的地并没有全部铺在一块，而是在输入电解电容处进行了连接，这样呢功率部分电流即使较大，它并不会影响单片机部分，因为电容是一个储能元件，即使功率部分出现一点波动，经过电容之后也不会对后级造成影响。 就好比一个大的水库，我们往里面扔一个石子，几乎不会对水位造成什么影响，这里也是一个道理。

然后，大家还要注意，在走地线的时候不要出现环路。

好了，那么关于该项目的PCB设计注意事项就给大家分享到这里啊，关于更多详细的内容，大家可以观看我们F1D部分的系列视频，最后给大家贴一下这个项目的最终PCB和3D效果图。

图10：F1D PCB示意图

图11：F1D 3D示意图

好了，那么本次文章的分享就给大家分享到这里啊，感谢大家的观看，我们下次再见，谢谢大家！

归一化在电机控制中究竟有什么用？

哈喽，大家好，今天我们来了解一下归一化在电机控制中的作用，那么首先我们需要先了解一下归一化的概念，这样才能更好的了解电机控制中为什么会经常用到归一化。

归一化就是将一个数据变换到（0，1）或者（-1，1）之间的小数，这样的话把数据范围都统一了，在一些算法处理中会更加方便，容易理解。

下面，我们举两个例子，这样可以更好的理解归一化，假设某个数据的变化范围是[0,1023],那么我们知道这个数据范围的最小值（xmin）是0，最大值（xmax）是1023，若我们得到的一个数据为x，那么归一化的方式就可以表示为：

如果x=1023，那么此时对1023归一化之后的结果为：

如果x=500，那么此时对500归一化之后的结果为：

接着我们再来看如果某个数据的变化范围是[-1023,1023],那么对于大于0的部分的归一化方式跟上面一致，归一化公式还是如下：

对于小于0的部分[-1023,0],归一化方式就可以表示为：

假设得到的数据x是-1023，那么可以得到此数据对应的归一化值为：

假设得到的数据x是-500，那么可以得到此数据对应的归一化值为：

通过以上实例分析，我们知道了归一化的实际实现方式，当我们有其它数据需要归一化时，就可以很容易的得到对应的归一化值。

在电机控制中，我们会对电角度进行归一化，我们都知道电角度的变化范围是0至360度，或者-180至180度，那么，同样我们也有两种归一化方式，对于用0-360度范围表示的电角度来说，归一化方式如下：

如果输入的角度是360度，那么得到的归一化值为1，如果输入的角度是180度，那么归一化值就是0.5，其它角度可以根据上面的角度归一化公式进行计算，这样对于0至360度范围的值就可以变化到0至1范围内了。

对于-180至180度范围表示的电角度来说，归一化的方式如下：

如果输入的电角度是180度，那么得到的归一化值为1，如果输入的电角度是-60度，那么得到的归一化值为-0.333333333，这样对于-180至180度范围的值就可以变化到-1至1范围内了。

归一化弄清楚之后，通过归一化，可以得到0至1或者-1至1之间的小数了，但是在电机控制中，大多数的单片机都没有浮点运算单元，而电机控制的算法中会用到大量的乘法运算，如果对于没有浮点运算单元的单片机来说，直接使用进行小数乘法或者小数除法，那么计算一个小数乘法或者计算一个小数乘法需要花费的时间是很长的。

假设我们整个电机控制算法全部执行完毕需要的时间是30us，那么如果一个小数乘法或者除法运算就花费了几微秒或者几十微秒，整个电机控制算法的就可能无法在30us以内完成了，那么对于一款没有浮点运算单元的单片机来说，又想实现小数乘法或者小数除法应该怎么做呢？

其实大部分的单片机有整数乘法，如果我们把小数乘法转化为整数形式乘法，那么也是可以实现小数乘法运算的，而且整数乘法运算的速度是比较快的，大部分的单片机都是单指令周期就可以实现，那么怎么实现把小数乘法转换为小数乘法呢？

接下来我们就要引入定点小数格式了，先给大家介绍一下定点小数格式的表示方法。

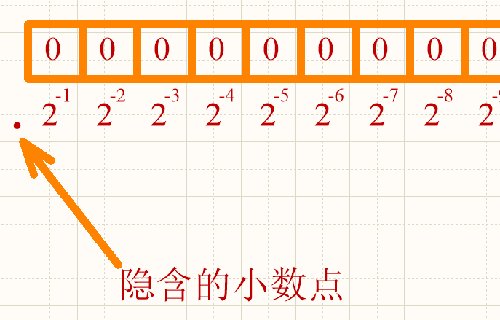
其定义为：约定单片机中所有数据的小数点位置是固定不变的。数据的最高位表示符号位，小数点是隐含在符号位之后的。这种格式通常被称为1.15或Q15格式，1.15中的1表示数据整数部分的位数，而15表示小数部分的位数。

下面用一个图示给大家说明一下这个定点小数的数据格式啊。

大家看这幅图啊。Q15格式的话，就是对于一个16位数来说，把最高位作为符号位，然后小数点是隐含在符号位后面的，剩余的15位作为数据位。

我们不妨根据上面这个数据格式来举例说明一下小数跟定点小数格式的转换方式，假设有一个数为0.5，那么对应的定点小数格式表示就是：

对应的16位数据格式的16进制表示为0x4000，十进制表示为16384。也就是说，对于-1至1范围的小数来说，16384表示0.5。

我们再假设有一个数据为-0.3，那么通过定点小数格式表示为：

计算的方式为：

上图对应的16位数据格式的16进制表示为0xD99A，十进制表示为-9830。也就是说，对于-1至1范围的小数来说，-9830表示-0.3。

以上是-1至1之间小数（有符号小数）的定点小数格式表示方式，那么在电机控制中有时还会用到无符号小数（0至1之间的小数），这个时候其实就是将Q15格式表示中的符号位去掉，所有的位都表示数据位，具体表示方式如下图所示：

我们不妨也对这种表示方式举个具体的例子来说明一下，假设小数为0.5，那么对应定点小数格式就表示为：

上图对应的16位数据格式的16进制表示为0x8000，十进制表示为32768。也就是说，对于0至1范围的小数来说，32768表示0.5。

假设得到的小数为0.7，那么对应定点小数格式就表示为：

计算的方式为：

上图对应的16位数据格式的16进制表示为0xB333，十进制表示为45875。也就是说，对于0至1范围的小数来说，45875表示0.7。

那么通过以上分析，我们知道了如何将一个小数表示为定点小数（整数）格式，经过这样的表示后，在我们程序编写中，就很好实现一个小数乘法了，最后给大家总结一下将小数转换为整数表示及将整数表示的小数转换为实际的小数对应的公式：

① 有符号小数负数部分转换为整数形式表示公式：

16位有符号数定点小数值 = 对应的小数 * 32768

② 无符号小数转换为整数形式表示公式：

16位无符号数定点小数值 = 对应的小数 * 65536

③ 有符号整数形式定点小数转换为实际小数表示公式：

实际小数值 = 16位有符号数定点小数值 / 32768

④ 无符号整数形式定点小数转换为实际小数表示公式：

实际小数值 = 16位有符号数定点小数值 / 65536

好了，那么本次文章就给大家分享到这里了，如果大家后期想关注更多的电机驱动方面的知识，可以持续关注我们张飞实战电子，谢谢大家！