无刷直流电机基础知识总结

今天给大家分享下电机控制中需要了解的一些基础知识，供大家参考学习。

一、三个基本定则

1.左手定则

左手定则是用来判断一个通电导体在磁场中受力方向的。具体受力方向如何判断，如下：

1）伸开左手，使大拇指和其余四指垂直；

2）手心面向N极，四指顺着电流的方向，那么大拇指所指方向就是导体受力方向。

力的大小计算公式为：F =    BILsinθ，其中B 为磁感应强度（单位 T），I 为电流大小（单位 A），L 为导体有效长度（单位 m），F 为力

的大小（单位 N），θ 为： B 和 I 的夹角。左手定则示意图如下图一所示：

图一：左手定则受力方向判断示意图

2.右手定则

由于通电导体的运动会切割磁感线，此时就会产生感应电动势，那么感应电动势的方向就可以用右手定则进行判定。右手定则具体内容如下所示：

右手平展，使大拇指与其余四指垂直，并且都跟手掌在一个平面内。把右手放入磁场中，让磁感线从掌心进入（当磁感线为直线时，相当于手心面向N极），大拇指指向导线运动方向，则四指所指方向为导线中感应电流（感应电动势）的方向。

感应电动势的大小可以通过公式E = vBLsinθ进行计算，其中v 为导体的运动速度（单位 m/s），B 为磁感应强度（单位 T），L 为导体长度（单位

m），θ 为B 和L的夹角。右手定则判定方向示意图如下图二所示：

图二：右手定则感应电动势方向判断示意图

3.右手螺旋定则

通电螺线管中流过电流时，会产生磁场，产生的磁场方向可以通过右手螺旋定则来进行判定。具体法则为：右手握住通电螺线管，使四指弯曲

与电流方向一致，大拇指所指的那一端就是通电螺旋管的 N 极。

右手螺旋定则判定示意图如下图三所示：

图三：右手螺旋定则判定磁场方向示意图

我们都知道，如果我们将一个小磁针放入磁场中，那么小磁针N方向的转动方向是往静止磁场的N方向转动，也就是说，当把小磁针放入磁场中时，静止后，小磁针的N方向跟磁场的N方向是一致的。

静止时刻的方向示意图如下图四所示：

图四：小磁针静止时的指向

二、电机基本概念

1.电机

电机（英文：Electric machinery，俗称“马达”）是指依据电磁感应定律实现电能转换或传递的一种电磁装置。下图所示为直流无刷电机。

图五：直流无刷电机

2.转子

电机工作时转动的部分称为转子。下图六所示为转子为永磁体的外转子电机转子结构。

图六：转子示意图

3.定子和绕组

电机工作时不转动的部分称为定子。如下图七所示为外转子无刷电机的定子示意图，定子结构上绕制了线圈。绕组就是定子上的线圈，通电后就会形成一定的磁场，从而推动转子旋转

图七：定子示意图

4.内转子电机

转子在定子内部，示意图如下图八所示：

图八：内转子电机示意图

5.外转子电机

转子在定子外部的电机称为外转子电机，如下图九为外转子电机示意图：

图九：外转子电机示意图

6.极数与极对数

极数是N极,S级的总数，一般都是指永磁体的磁极数,下图十所示的电机有6极。极对数是 一个南极(S极) ，一个北极(N极) ，算一对磁极，极对数=级数÷2,下图十所示的电机有3对极。

图十：极数及极对数介绍示意图

7.机械角度与电角度

机械角度就是数学中的“空间几何角度”，恒等于360度。电角度指磁场每转过一对磁极,导体的电动势变化一个周期,定义一个周期为360°电角度。

电角度=机械角度*极对数

若电机有K对极,那么整个定子内圆有K*360°电角度,右图电机有4对极,因此一圈是360°机械角度,1440°电角度

图十一：机械角度与电角度介绍示意图

8. KV值

KV值是指输入电压每增加 1 伏特，无刷电机空转转速增加值，转速=KV*电压。比如KV=1000,那么当输入电压10V时,空转转速就是10000rpm  (rpm=转/分钟)。同系列同外形尺寸的无刷电机，根据绕线匝数的多少，会表现出不同的 KV 特性。绕线匝数多的，KV 值低，最高输出电流小，扭力大；绕线匝数少的，KV 值高，最高输出电流大，扭力小。

图十二：KV值示意图

9. 霍尔传感器

霍尔传感器感应磁场方向,并输出高低电平(”1”和”0”),根据霍尔传感器的输出值,就能确定转子的位置。下图十三表示霍尔安装及霍尔波形示意图：

图十三：霍尔安装及霍尔波形示意图

10. 死点

转子在死点位置,电机无启动力矩,一般是转子磁场与定子磁场方向平行，如下图十四所示表示死点示意图：

图十四：死点位置示意图

今天的内容就给大家分享到这里，下次有机会再继续给大家分享更多关于电机相关的基础知识，谢谢大家！

编码器的分类及增量式光电编码器的工作原理

一、编码器介绍

编码器是一种传感器，主要是用来检测机械运动的速度、位置、角度、距离或计数，它是一种集光、机、电为一体的数字化检测装置，它具有分辨率高、精度高、结构简单、体积小、使用可靠、易于维护、性价比高等优点。

近些年来，它发展为一种成熟的多规格、高性能的系列工业化产品，在数控机床、机器人、雷达、光电经纬仪、地面指挥仪、高精度闭环调速系统、伺服系统等诸多领域中得到了广泛的引用。

那么，光电编码器可以定义为：一种通过光电转换，将输至轴上的机械、几何位移量转换成脉冲或数字量的传感器，它主要用于速度或位置（角度）的检测。比较典型的光电编码器由码盘（Disk）、检测光栅（Mask）、光电转换电路（包括光源、光敏器件、信号转换电路）、机械部件等组成。

二、编码器的分类

对于编码器的分类，可以用下图一的结构来表示：

图一：编码器的分类

上图一所示的分类只是其中一种分类方法。另外，按照编码器运动部件的运动方式来分，可以分为旋转式和直线式两种。根据检测原理，编码器可以分为光学式、磁式、感应式和电容式。旋转式光电编码器容易做成全封闭型式，易于实现小型化，传感长度较长，具有较长的环境适用能力，因而在实际工业生产中得到广泛的应用。

三、编码器中常用的术语

1、输出脉冲数/转

旋转编码器转一圈所输出的脉冲数，对于光学式旋转编码器，通常与旋转编码器内部光栅的槽数相同（也可在电路上使输出脉冲数增加到槽数的2倍，4倍）。

2、分辨率

分辨率表示旋转编码器的主轴旋转一周，读出位置数据的最大等分数。绝对值型不以脉冲形式输出，而已代码形式表示当前主轴位置（角度）。与增量型不同，相当于增量型的“输出脉冲/转”。

3、光栅

光学式旋转编码器，其光栅有金属和玻璃两种。如果式金属制成的，会开有通光孔槽；如果是玻璃制成的，是在玻璃表面涂了一层遮光膜，在此上面设有透明线条（槽）。在槽数少的场合，可以在金属圆盘上用冲床加工或腐蚀法开槽。在耐冲击型编码器上使用了金属的光栅。玻璃制的与金属制的光栅相比不耐冲击，因此在使用上请注意，不要将冲击直接施加于编码器上。

4、最大响应频率

是在1秒内能响应的最大脉冲数（例：最大响应频率为2KHz，即1秒内可响应2000个脉冲），公式如下：

最大响应转速（RPM）/ 60 *（脉冲数/转）=输出频率Hz

5、最大响应转速

是指可响应的最高转速，在此转速下发生的脉冲都可响应，公式如下：

最大响应频率（Hz）/ （脉冲数/转） * 60 = 轴的转速RPM

6、输出电压

是指输出脉冲的电压。输出电压会因输出电流的变换而有所变化。

7、格雷码

格雷码是高级数据，因为是单元距离和循环码，所以很安全。每步只有一位变化。数据处理时，格雷码必须转换成二进制码。

8、转速

改速度指示编码器的机械载荷限制。如果超出该限制，将对轴承使用寿命产生负面影响，另外信号也可能中断。

四、增量式编码器的工作原理

1、基本构造及特点

增量式光电编码器的特点是没产生一个输出脉冲信号就对应于一个增量位移，但是不能通过输出脉冲区别出在哪个位置上的增量。它能够产生与位移增量等值的脉冲信号，其作用是提供一种对连续位移量离散化或增量化以及位移变化（速度）的传感方法，它相对于某个基准点的相对位置增量，不能够直接检测出轴的绝对位置信息。一般来说，增量式光电编码器输出A、B两相互差90读电角度的脉冲信号（也即是两组正交输出信号），从而可以方便地判断出旋转方向。同时还有用作参考零位的Z相标志（指示）脉冲信号，码盘每旋转一周，只发出一个标志信号。标志脉冲通常用来指示机械位置或对积累量清零。

增量式光电编码器主要由光源、光栅板（码盘）、固定光栅（检测光栅）、光敏管（光电检测器件）和转换电路组成，如下图二所示：

图二：增量式光电编码器的组成

在光栅板上刻有节距相等的辐射状透光缝隙，相邻两个透光缝隙之间代表一个增量周期；检测光栅上刻有A、B两组与光栅板相对应的透光缝隙，用以通过或阻挡光源和光电检测器件之间的光线。它们的节距和码盘上的节距相等。并且两组透光缝隙错开1/4节距，使得光电检测器件输出的信号在相位上相差90度电角度。当码盘随着被测轴转动时，检测光栅不动，光线透过码盘和检测光栅上透过缝隙照射到光电检测器件上，光电检测器件就输出两组相位相差90度电角度的近似于正弦波的电信号，电信号经过转换电路的信号处理，可以得到被测轴的转角或速度信息。增量式光电编码器输出信号波形如下图三所示：

图三：增量式光电编码器的输出信号波形

2、作用原理

A、B两点对应两个光敏接受管，A、B两点间距为S2,角度码盘的光栅间距分别为S0和S1。当角度码盘以某个速度匀速转动时，那么可知输出波形图中的S0:S1:S2比值相同，同理角度码盘以其它的速度匀速转动时，输出波形中的S0:S1:S2比值与实际图的S0:S1:S2比值仍然相同。增量式光电编码器内部工作原理示意图如下图四表示：

图四：增量式光电编码器内部工作原理

如果角度码盘做变速运动，把它看成多个运动周期的组合，那么每个运动周期输出波形图中的S0:S1:S2比值与实际图的S0:S1:S2比值仍然相同。通过输出波形我们可知每个运动周期的时序图如下图五表示：

图五：时序图

我们把当前的A、B输出值保存起来，与下一个A、B输出值做比较，就可以轻易的知道角度码盘的运动方向，如果光栅S0等于S1时，也就是S0和S1弧度夹角相同，且S2等于S0的1/2，那么就可得到此次角度码盘运动位移角度为S0弧度夹角的1/2，除以所消耗的时间，就可以得到此次角度码盘运动位移角速度。

以上就是增量式光电编码器的工作原理。那么本篇文章就给大家介绍这么多，后面有机会再给大家介绍绝对式编码器的组成及其工作原理。

归一化在电机控制中究竟有什么用？

哈喽，大家好，今天我们来了解一下归一化在电机控制中的作用，那么首先我们需要先了解一下归一化的概念，这样才能更好的了解电机控制中为什么会经常用到归一化。

归一化就是将一个数据变换到（0，1）或者（-1，1）之间的小数，这样的话把数据范围都统一了，在一些算法处理中会更加方便，容易理解。

下面，我们举两个例子，这样可以更好的理解归一化，假设某个数据的变化范围是[0,1023],那么我们知道这个数据范围的最小值（xmin）是0，最大值（xmax）是1023，若我们得到的一个数据为x，那么归一化的方式就可以表示为：

如果x=1023，那么此时对1023归一化之后的结果为：

如果x=500，那么此时对500归一化之后的结果为：

接着我们再来看如果某个数据的变化范围是[-1023,1023],那么对于大于0的部分的归一化方式跟上面一致，归一化公式还是如下：

对于小于0的部分[-1023,0],归一化方式就可以表示为：

假设得到的数据x是-1023，那么可以得到此数据对应的归一化值为：

假设得到的数据x是-500，那么可以得到此数据对应的归一化值为：

通过以上实例分析，我们知道了归一化的实际实现方式，当我们有其它数据需要归一化时，就可以很容易的得到对应的归一化值。

在电机控制中，我们会对电角度进行归一化，我们都知道电角度的变化范围是0至360度，或者-180至180度，那么，同样我们也有两种归一化方式，对于用0-360度范围表示的电角度来说，归一化方式如下：

如果输入的角度是360度，那么得到的归一化值为1，如果输入的角度是180度，那么归一化值就是0.5，其它角度可以根据上面的角度归一化公式进行计算，这样对于0至360度范围的值就可以变化到0至1范围内了。

对于-180至180度范围表示的电角度来说，归一化的方式如下：

如果输入的电角度是180度，那么得到的归一化值为1，如果输入的电角度是-60度，那么得到的归一化值为-0.333333333，这样对于-180至180度范围的值就可以变化到-1至1范围内了。

归一化弄清楚之后，通过归一化，可以得到0至1或者-1至1之间的小数了，但是在电机控制中，大多数的单片机都没有浮点运算单元，而电机控制的算法中会用到大量的乘法运算，如果对于没有浮点运算单元的单片机来说，直接使用进行小数乘法或者小数除法，那么计算一个小数乘法或者计算一个小数乘法需要花费的时间是很长的。

假设我们整个电机控制算法全部执行完毕需要的时间是30us，那么如果一个小数乘法或者除法运算就花费了几微秒或者几十微秒，整个电机控制算法的就可能无法在30us以内完成了，那么对于一款没有浮点运算单元的单片机来说，又想实现小数乘法或者小数除法应该怎么做呢？

其实大部分的单片机有整数乘法，如果我们把小数乘法转化为整数形式乘法，那么也是可以实现小数乘法运算的，而且整数乘法运算的速度是比较快的，大部分的单片机都是单指令周期就可以实现，那么怎么实现把小数乘法转换为小数乘法呢？

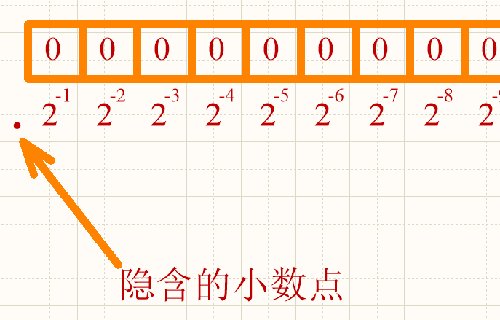
接下来我们就要引入定点小数格式了，先给大家介绍一下定点小数格式的表示方法。

其定义为：约定单片机中所有数据的小数点位置是固定不变的。数据的最高位表示符号位，小数点是隐含在符号位之后的。这种格式通常被称为1.15或Q15格式，1.15中的1表示数据整数部分的位数，而15表示小数部分的位数。

下面用一个图示给大家说明一下这个定点小数的数据格式啊。

大家看这幅图啊。Q15格式的话，就是对于一个16位数来说，把最高位作为符号位，然后小数点是隐含在符号位后面的，剩余的15位作为数据位。

我们不妨根据上面这个数据格式来举例说明一下小数跟定点小数格式的转换方式，假设有一个数为0.5，那么对应的定点小数格式表示就是：

对应的16位数据格式的16进制表示为0x4000，十进制表示为16384。也就是说，对于-1至1范围的小数来说，16384表示0.5。

我们再假设有一个数据为-0.3，那么通过定点小数格式表示为：

计算的方式为：

上图对应的16位数据格式的16进制表示为0xD99A，十进制表示为-9830。也就是说，对于-1至1范围的小数来说，-9830表示-0.3。

以上是-1至1之间小数（有符号小数）的定点小数格式表示方式，那么在电机控制中有时还会用到无符号小数（0至1之间的小数），这个时候其实就是将Q15格式表示中的符号位去掉，所有的位都表示数据位，具体表示方式如下图所示：

我们不妨也对这种表示方式举个具体的例子来说明一下，假设小数为0.5，那么对应定点小数格式就表示为：

上图对应的16位数据格式的16进制表示为0x8000，十进制表示为32768。也就是说，对于0至1范围的小数来说，32768表示0.5。

假设得到的小数为0.7，那么对应定点小数格式就表示为：

计算的方式为：

上图对应的16位数据格式的16进制表示为0xB333，十进制表示为45875。也就是说，对于0至1范围的小数来说，45875表示0.7。

那么通过以上分析，我们知道了如何将一个小数表示为定点小数（整数）格式，经过这样的表示后，在我们程序编写中，就很好实现一个小数乘法了，最后给大家总结一下将小数转换为整数表示及将整数表示的小数转换为实际的小数对应的公式：

① 有符号小数负数部分转换为整数形式表示公式：

16位有符号数定点小数值 = 对应的小数 * 32768

② 无符号小数转换为整数形式表示公式：

16位无符号数定点小数值 = 对应的小数 * 65536

③ 有符号整数形式定点小数转换为实际小数表示公式：

实际小数值 = 16位有符号数定点小数值 / 32768

④ 无符号整数形式定点小数转换为实际小数表示公式：

实际小数值 = 16位有符号数定点小数值 / 65536

好了，那么本次文章就给大家分享到这里了，如果大家后期想关注更多的电机驱动方面的知识，可以持续关注我们张飞实战电子，谢谢大家！

霍尔传感器介绍

霍尔传感器是一种磁传感器。用它可以检测磁场及其变化，可在各种与磁场有关的场合中使用。霍尔传感器以霍尔效应为其工作基础，是由霍尔元件和它的附属电路组成的集成传感器。霍尔传感器在工业生产、交通运输和日常生活中有着非常广泛的应用。

一、霍尔效应 霍尔元件 霍尔传感器

（一）霍尔效应

如图1所示，在半导体薄片两端通以控制电流I，并在薄片的垂直方向施加磁感应强度为B的匀强磁场，则在垂直于电流和磁场的方向上，将产生电势差为UH的霍尔电压，它们之间的关系为：

式中d 为薄片的厚度，k称为霍尔系数，它的大小与薄片的材料有关。

上述效应称为霍尔效应，它是德国物理学家霍尔于1879年研究载流导体在磁场中受力的性质时发现的。

（二）霍尔元件

根据霍尔效应，人们用半导体材料制成的元件叫霍尔元件。它具有对磁场敏感、结构简单、体积小、频率响应宽、输出电压变化大和使用寿命长等优点，因此，在测量、自动化、计算机和信息技术等领域得到广泛的应用。

（三）霍尔传感器

由于霍尔元件产生的电势差很小，故通常将霍尔元件与放大器电路、温度补偿电路及稳压电源电路等集成在一个芯片上，称之为霍尔传感器。

霍尔传感器也称为霍尔集成电路，其外形较小，如图2所示，是其中一种型号的外形图。

二、霍尔传感器的分类

霍尔传感器分为线性型霍尔传感器和开关型霍尔传感器两种。

（一）线性型霍尔传感器由霍尔元件、线性放大器和射极跟随器组成，它输出模拟量。

（二）开关型霍尔传感器由稳压器、霍尔元件、差分放大器，斯密特触发器和输出级组成，它输出数字量。

三、霍尔传感器的特性

（一）线性型霍尔传感器的特性

输出电压与外加磁场强度呈线性关系，如图3所示，可见，在B1～B2的磁感应强度范围内有较好的线性度，磁感应强度超出此范围时则呈现饱和状态。

（二）开关型霍尔传感器的特性

如图4所示，其中BOP为工作点“开”的磁感应强度，BRP为释放点“关”的磁感应强度。

当外加的磁感应强度超过动作点Bop时，传感器输出低电平，当磁感应强度降到动作点Bop以下时，传感器输出电平不变，一直要降到释放点BRP时，传感器才由低电平跃变为高电平。Bop与BRP之间的滞后使开关动作更为可靠。

另外还有一种“锁键型”（或称“锁存型”）开关型霍尔传感器，其特性如图5所示。

当磁感应强度超过动作点Bop时，传感器输出由高电平跃变为低电平，而在外磁场撤消后，其输出状态保持不变（即锁存状态），必须施加反向磁感应强度达到BRP时，才能使电平产生变化。

四、霍尔传感器的应用

按被检测对象的性质可将它们的应用分为：直接应用和间接应用。前者是直接检测受检对象本身的磁场或磁特性，后者是检测受检对象上人为设置的磁场，这个磁场是被检测的信息的载体，通过它，将许多非电、非磁的物理量，例如速度、加速度、角度、角速度、转数、转速以及工作状态发生变化的时间等，转变成电学量来进行检测和控制。

（一）线性型霍尔传感器主要用于一些物理量的测量。例如：

1、电流传感器

由于通电螺线管内部存在磁场，其大小与导线中的电流成正比，故可以利用霍尔传感器测量出磁场，从而确定导线中电流的大小。利用这一原理可以设计制成霍尔电流传感器。其优点是不与被测电路发生电接触，不影响被测电路，不消耗被测电源的功率，特别适合于高电压、大电流传感。

霍尔电流传感器工作原理如图6所示，标准圆环铁芯有一个缺口，将霍尔传感器插入缺口中，圆环上绕有线圈，当电流通过线圈时产生磁场，则霍尔传感器有信号输出。

2、位移测量

如图7所示，两块永久磁铁同极性相对放置，将线性型霍尔传感器置于中间，其磁感应强度为零，这个点可作为位移的零点，当霍尔传感器在Z轴上作△Z位移时，传感器有一个电压输出，电压大小与位移大小成正比。

如果把拉力、压力等参数变成位移，便可测出拉力及压力的大小，如图8所示，是按这一原理制成的力传感器。

（二）开关型霍尔传感器主要用于测转数、转速、风速、流速、接近开关、关门告知器、报警器、自动控制电路等。

1、测转速或转数

如图9所示，在非磁性材料的圆盘边上粘一块磁钢，霍尔传感器放在靠近圆盘边缘处，圆盘旋转一周，霍尔传感器就输出一个脉冲，从而可测出转数（计数器），若接入频率计，便可测出转速。

如果把开关型霍尔传感器按预定位置有规律地布置在轨道上，当装在运动车辆上的永磁体经过它时，可以从测量电路上测得脉冲信号。根据脉冲信号的分布可以测出车辆的运动速度。

2、各种实用电路

开关型霍尔传感器尺寸小、工作电压范围宽，工作可靠，价格便宜，因此获得极为广泛的应用。下面列举两个实用电路加以说明：

电路1 防盗报警器：

如图10所示，将小磁铁固定在门的边缘上，将霍尔传感器固定在门框的边缘上，让两者靠近，即门处于关闭状态时，磁铁靠近霍尔传感器，输出端3为低电平，当门被非法撬开时，霍尔传感器输出端3为高电平，非门输出端Y为低电平，继电器J吸合，Ja闭合，蜂鸣器得电后发出报警声音。

电路2 公共汽车门状态显示器：

使用霍尔传感器，只要再配置一块小永久磁铁就很容易做成车门是否关好的指示器，例如公共汽车的三个门必须关闭，司机才可开车。电路如图11所示，三片开关型霍尔传感器分别装在汽车的三个门框上，在车门适当位置各固定一块磁钢，当车门开着时，磁钢远离霍尔开关，输出端为高电平。若三个门中有一个未关好，则或非门输出为低电平，红灯亮，表示还有门未关好，若三个门都关好，则或非门输出为高电平，绿灯亮，表示车门关好，司机可放心开车。

反电动势到底该如何来理解？

电机中的反电动势是如何产生的呢？要了解这个问题，我们需要回顾一下高中时学过的电磁学知识，在电磁学中我们学到过感应电动势，感应电动势又分为动生电动势和感生电动势两类。

动生电动势是一种由于导体在磁场中运动而在导体内部产生的电动势。感生电动势是一种由于磁场变化而静止导体中产生的一种电动势。

那么我们直流无刷电机中产生的反电动势属于感应电动势中的哪一类呢？因此我们就需要了解一下直流无刷电机的构造了。下图一是一个外转子直流无刷电机：

图一：外转子直流无刷电机示意图

那么从上图一中的电机组成来看，我们知道定子是线圈组成，也就是说导体是静止的，而转子由永磁体组成，永磁体是转动的，那么当永磁体转动时，对于线圈来说就是线圈的磁场发生了变化，因此对于这样构造的直流无刷电机来说，产生的感应电动势就是感生电动势。我们也可以知道，感生电动势的产生是转子永磁体对定子线圈的一个作用。

从上面我们知道，随着电机转子（永磁体）的转动，会感生出一个感生电动势，这个感生电动势的方向可以根据楞次定律（感应电流的磁场总要阻碍引起感应电流的磁通量的变化）来进行判断。

图二：外加磁场靠近线圈，磁通量增加时感应电动势方向示意图

图三：外加磁场远离线圈，磁通量减小时感应电动势方向示意图

从上图二图三我们可以知道，当线圈磁通量增加，感应电流产生的磁场方向要阻碍磁通量的增加，当线圈磁通量减小时，感应电流产生的磁场方向要阻碍磁通量的减小。

那么这个感应电动势的方向跟线圈外加电压的方向是相反的，所以通常在电机中把这个感应电动势称为反电动势。这就是反电动势的来源。

通过以上分析，我们知道了转子是永磁体，定子是绕组线圈的直流无刷电机产生的感生电动势就是电机的反电动势，那么根据感生电动势E的公式：

由以上公式可以知道电机绕组中的反电动势的大小跟它的单位时间内的磁通量的变化量成正比。也就是说，在Δt固定的情况下，磁通量变化越大，那么反电动势就越大，反之磁通量变化越小，那么反电动势就越小。

我们知道磁通量的公式如下：

其中，B是磁感应强度，S是线圈平面面积，θ是线圈平面法线与磁感应强度B的夹角。

图四：坐标系及角度定义示意图

为了方便分析，我们假设坐标系及角度定义如上图四所示，从磁通量公式我们可以知道，定子绕组中的磁通量是按正弦规律变化的。

图五：转子与定子线圈通电示意图

在上图五中，转子永磁体磁力线方向与N方向一致，而线圈平面法线方向水平向右，如下图六所示：

图六：磁感应强度方向与线圈平面法线方向示意图

我们可以根据磁通量的公式知道，此时线圈磁通量为0。

图七：转子与定子线圈通电示意图

当转子转动到上图七所示的位置时，此时夹角θ为0，根据磁通量的公式可知，此时磁通量是最大的，因此对于一个固定的定子绕组来说，当转子转动一周，随着磁感应强度与线圈平面的夹角不同（也就是转子的位置角不同）那么磁通量的变化是按照正弦规律变化的。

图八：磁通量曲线示意图

从图八我们可以知道，在0度位置时，磁通量最大，但是磁通量的变化率最小为0（斜率为0），感应电动势为0，在90度时，磁通量为0，但是磁通量的变化率最大（斜率最大），感应电动势最大，在180度时，磁通量最大，磁通量的变化率又为0（斜率为0），感应电动势为0，在270度时，磁通量为0，但是磁通量的变化率最大（斜率反向最大），感应电动势最大。

也就是上式中为单位时间内的磁通量变化，这个变化在数学中可以用求导来表示，也即是上式我们可以写成为：

因此我们可以根据上式画出感应电动势（反电动势）的波形，如下图九所示：

图九：感应电动势波形示意图

那么以上就是对电机中的反电动势的一些理解，仅供大家参考，起个抛砖引玉的作用，希望大家可以利用以上分析，对反电动势的理解更加深入、更加透彻、更加清晰。本篇文章就给大家分享到这里，谢谢大家！